[GIT] indeterminism GRACELI TRANSCENDENTE.

quinta-feira, 9 de outubro de 2014

Cálculo e geometria transcendente.

para espirais variacionais e transcendentes.

onde temos pontos nulos e inexistentes seguino de valores alternados de progressões.

n = r *θ

\Sigma

{\int}

i [logx/x * r *θ [a,P,0]]

i = i = 1* logx/x * r *θ [a,P,0] [n]

r *θ = raio e ângulo.

Cálculo e geometria transcendente.

n = n =

f:I\to\mathbb{R}

y = f(x)

\Sigma

{\int}

i [logx/x * [a,P,0]]

i = i = 1* logx/x * [a,P,0] [n][

f:I\to\mathbb{R}

y = f(x)

\scriptstyle f(x)=1 + x\sin x^2

\Sigma

{\int}

i [logx/x * [a,P,0]][

\scriptstyle f(x)=1 + x\sin x^2

]

i = i = 1* logx/x * [a,P,0] [n]

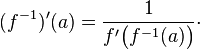
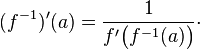
(f^{-1})'(a)=\frac1{f'\bigl(f^{-1}(a)\bigr)}\cdot

\Sigma

{\int}

i [logx/x * [a,P,0]

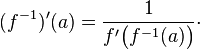(f^{-1})'(a)=\frac1{f'\bigl(f^{-1}(a)\bigr)}\cdot

]

i = i = 1* logx/x * [a,P,0] [n]

quinta-feira, 9 de outubro de 2014